O problema consiste em determinarmos q.
Desenvolvendo a PA
Como a, b e c estão numa sequência de PA então há uma constante r na composição destes números os quais podemos reescrevê-los da seguinte forma:
Assim, somando a + b + c = (b - r) + b + (b + r) = 3b = 21
Logo,
b = 7
Precisamos agora determinar r.
Passando para a PG
Como temos a sequência {(a + c)/2b; c - a; b + c} em PG então o produto dos extremos é igual ao quadrado do termo médio. Assim,
Comparando (1) com (2):
Como b = 7,
Usando Bhaskara:
Como por hipótese a PA é crescente logo, apenas
r = 2 satisfaz.
Determinando q
Como
Podemos desta forma usar
Que fica
Comparamos (3) com (1)
Como b = 7 e r = 2 temos que
q = (2.7 + 2)/2.2 = 16/4 = 4
Portanto letra D.



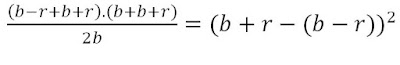







Pessoal, podemos fazer a sequência da PA igual a (a, b, c) = (a, a + r, a + 2r) e chegamos no mesmo resultado.
ResponderExcluirCaramba, ainda to mastigando.... =.= mas com certeza uma hora eu vou entender...
ResponderExcluirArthur, pegue a ideia geral e tente resolver o problema sem olhar o passo a passo. Nas travadas reveja a solução. Recomece do início até você entender. Um abraço.
ExcluirAh, só pra constar, a PA dá a sequência (5, 7, 9) e a PG dá (1, 4, 16).
Excluir