Boa noite, Pessoal!
Sabemos que numa função quadrática de representação f(x) = ax2
+ bx + c , tem por coordenadas do seu vértice o ponto
V(-b/2a, -Δ/4a)
ou numa representação
gráfica:
Fica a pergunta, de onde tiramos esta relação?
Observemos que o x do vértice fica exatamente no ponto médio das duas raízes:
Vamos relembrar os valores das raízes?
Desta forma, o x do vértice será (x' + x")/2. Vamos fazer as contas?
E assim,
Agora, para determinarmos o y do vértice aplicamos o x do vértice na função f(x) = ax2
+ bx + c. Que fica:
f(xv)
= a(-b/2a)2 + b(-b/2a) + c
f(xv)
= ab2/4a2 – b2/2a + c
f(xv)
= b2/4a – b2/2a + c
O MMC
(4a, 2a) = 4a e assim,
Como Δ = b2
-4ac então,
Portanto,
V(-b/2a, -Δ/4a)








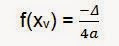
Nenhum comentário:
Postar um comentário