
Boa noite, Pessoal!
CONTINUANDO A RESOLUÇÃO!
A primeira coisa a ser feita para encaminhar a solução deste problema é determinar a função quadrática que contém estes 3 pontos A(-1, 0), B(5, 0) e C(-2, -7).
Para isto podemos usar três abordagens:
b) Uma matriz estendida escalonada ou
Os encaminhamentos em a) e b) tem um caráter mais geral. Já c) só vale pois os pontos A e B serem raízes da função procurada. A solução em c) é mais rápida e mais intuitiva.
Irei resolver a) e b) e deixarei c) para vocês, ok?
SOLUÇÃO USANDO MATRIZ ESTENDIDA ESCALONADA
A função que buscamos tem a seguinte forma f(x) = ax2 + bx + c. E, desta forma, temos que determinar os valores de a, b e c.
Pegamos os valores de x e y dos pontos A, B e C e reescrevemos a função f(x).
Para A(-1, 0):
a(-1)2 +b(-1) + c = 0 → a – b + c = 0 (1)
Para B(5, 0):
a.52 + 5b + c = 0 → 25a + 5b + c = 0 (2) e
Para C(-2, -7):
a(-2)2 + b(-2) + c = -7 → 4a – 2b + c = -7 (3).
Agora temos três equações com três incógnitas em (1), (2) e (3).
Aqui já começam as diferenças. Observem!
Do sistema de equações acima formamos a seguinte matriz estendida:
 |
| Matriz 1 |
Cada linha da matriz representa uma equação sem as incógnitas a, b ou c. O que vamos fazer é usar somas e produtos em cada linha para chegamos aos dois possíveis resultados como abaixo:
Ou,
Pretendemos ter um triângulo de zeros superior direito ou inferior esquerdo usando somas e produtos.
Observem que aij representa o elemento "a" da linha i e da coluna j. Exemplo, a23 representa o
elemento "a" da linha 2 e coluna 3. Na matriz 1 este elemento é o número 1.
Vamos começar?
1) Pegamos a
linha 1, multiplicamos por -1 e somamos termo a termo com a linha 3. A linha 1
multiplicada por -1 fica (-1, 1, -1, 0). Somada com (4, -2, 1, -7) dá resultado
(4-1, -2 + 1, 1 – 1, -7 + 0) = (3, -1, 0, -7). Que fica assim:
2)
Pegamos a
linha 3, multiplicamos por -1 e somamos termo a termo com a linha 2. A linha 3
multiplicada por -1 fica (-4, 2, -1, 7). Somada com (25, 5, 1, 0) dá resultado
(-4 + 25, 2 + 5, -1 + 1, 7 + 0) = (21, 7, 0, 7).
3)
Dividimos
a linha 2 por 7 que fica:
2)
Somamos a
linha dois com a 3 que dá (3 + 3, -1 +1, 0 + 0, -7 + 1) = (6, 0, 0, -6). Este
resultado dividimos por 6 que fica (1, 0, 0, -1).
Conseguimos o nosso triângulo de zeros. E agora?
Reescrevemos as equações para que possamos visualizar.
Logo, a = -1 (pela primeira linha);
3a + b = 1
3(-1) + b = 1
-3 + b = 1
b = 1 + 3
b= 4 (pela segunda linha) e
4a - 2b + c = -7
4(-1) - 2(4) + c = -7
-4 - 8 + c = - 7
- 12 + c = -7
c = -7 +12
c = 5 (pela linha 3).
A continuação a partir daqui é idêntica a que foi feita pelo método do Sistema de Equações Lineares e a resposta então fica, depois de resolvido tudo, que a letra certa é a B onde o máximo da função é 9.
Só resta agora a resolução por Polinômios que deixo para vocês!
Um abraço fraternal!




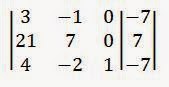



Nenhum comentário:
Postar um comentário