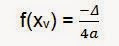Já há algum tempo que circula pelo facebook um "Teste de Inteligência". Segue abaixo:
E há muitas pessoas que dão muitas respostas diferentes. Uns dizem que a solução é 27. Outros que é 37 e por aí vai. Aproveito o espaço deste blog para tentar lançar uma luz sobre a questão e fazer outras considerações que considero relevantes.
f(6, 4)=6*101 - 4*99 =
210;
f(9,
2)=9*101 - 2*99 = 711;
f(8,
5)=8*101 -5*99 = 313 e
f(5,
2)=5*101 - 2*99 = 307.
Portanto,
5 + 2 = 307.
Observemos
que + é uma operação e que é definida pela álgebra f(x, y) = 101x - 99y. E de
onde tiramos esta relação? Notem que o primeiro número da centena é a subtração
de x por y e que a dezena é a soma de x com y. Assim fica, f(x, y) = 100 * (x -
y) + (x + y). Simplificando fica,
f(x, y) = 101x - 99y
E se quisermos
determinar um número inteiro
k quanto solução da função?
Determinando o zero.
Não é único e pode ser formado pelo par (0, 0) ou pelo par (99, 101).
Vamos
verificar?
f(0, 0) = 101.0 - 99.0 = 0
f(99, 101) = 101.99 - 99.101 = 0
f(99, 101) = 101.99 - 99.101 = 0
E a unidade?
A
unidade existe só que também não é única. Podemos determinar um exemplo, x =
-49 e y = -50. f( -49, -50) = -49.101 - (-50).99 = -4949 + 4950 = 1.
Como podemos
determinar uma tripla da forma (-49, -50, 1) então podemos mapear todo o
conjunto dos inteiros simplesmente fazendo k(-49, -50, 1) = (-49k, -50k, k), onde k é o inteiro
que queremos determinar usando apenas inteiros. Um exemplo, k = 27:
f(-49.27,
-50.27) = f(-1323, -1350) = -1323.101 - (-1350).99 =
- 133623 + 133650 = 27!!!
Portanto,
(-1323) + (-1350) = 27.
Como determinarmos um procedimento para chegarmos a k?
O exposto acima não explica logicamente como chegamos ao resultado do vetor (-49, -50, 1) e posteriormente (-49k, -50k, k). Para essa determinação usaremos Equações Diofantinas.
Queremos encontrar uma fórmula geral que equacione a equação
101x - 99y = k (1), com k Є Z.
O primeiro passo é
determinarmos um caso particular. Para isso fazendo k = 1. E assim fica:
101x – 99y = 1
O MDC(99, 101) = 1.
O passo seguinte é reconstruirmos a equação acima usando o algoritmo da
divisão. Logo,
101 = 1.99 + 2 → 2 = 101 – 1.99 (2)
Usamos o resto da primeira divisão como divisor de 99, assim,
99 = 2.49 + 1 (3)
Comparando (2) com (3) teremos,
99 = (101 – 1.99).49 + 1
99 = 49.101 – 49.99 + 1
99 + 49.99 – 49.101 = 1
50.99 – 49.101 = 1 (4)
Como a equação é escrita da forma 101x – 99y = 1 então reescrevemos,
– 49.101 – ( - 50)99 = 1
Como queremos determinar uma solução particular para k basta
multiplicarmos (4) por esta constante.
(-49k)101 – ( - 50k)99 = k
Assim,
Desta forma, a solução geral para um k qualquer fica:
Com
t Є Z.